Note
Go to the end to download the full example code. or to run this example in your browser via Binder
Multi-dimensional scaling#
An illustration of the metric and non-metric MDS on generated noisy data.
# Authors: The scikit-learn developers
# SPDX-License-Identifier: BSD-3-Clause
Dataset preparation#
We start by uniformly generating 20 points in a 2D space.
import numpy as np
from matplotlib import pyplot as plt
from matplotlib.collections import LineCollection
from sklearn import manifold
from sklearn.decomposition import PCA
from sklearn.metrics import euclidean_distances
# Generate the data
EPSILON = np.finfo(np.float32).eps
n_samples = 20
rng = np.random.RandomState(seed=3)
X_true = rng.randint(0, 20, 2 * n_samples).astype(float)
X_true = X_true.reshape((n_samples, 2))
# Center the data
X_true -= X_true.mean()
Now we compute pairwise distances between all points and add a small amount of noise to the distance matrix. We make sure to keep the noisy distance matrix symmetric.
# Compute pairwise Euclidean distances
distances = euclidean_distances(X_true)
# Add noise to the distances
noise = rng.rand(n_samples, n_samples)
noise = noise + noise.T
np.fill_diagonal(noise, 0)
distances += noise
Here we compute metric and non-metric MDS of the noisy distance matrix.
mds = manifold.MDS(
n_components=2,
max_iter=3000,
eps=1e-9,
n_init=1,
random_state=42,
dissimilarity="precomputed",
n_jobs=1,
)
X_mds = mds.fit(distances).embedding_
nmds = manifold.MDS(
n_components=2,
metric=False,
max_iter=3000,
eps=1e-12,
dissimilarity="precomputed",
random_state=42,
n_jobs=1,
n_init=1,
)
X_nmds = nmds.fit_transform(distances)
Rescaling the non-metric MDS solution to match the spread of the original data.
To make the visual comparisons easier, we rotate the original data and both MDS solutions to their PCA axes. And flip horizontal and vertical MDS axes, if needed, to match the original data orientation.
# Rotate the data
pca = PCA(n_components=2)
X_true = pca.fit_transform(X_true)
X_mds = pca.fit_transform(X_mds)
X_nmds = pca.fit_transform(X_nmds)
# Align the sign of PCs
for i in [0, 1]:
if np.corrcoef(X_mds[:, i], X_true[:, i])[0, 1] < 0:
X_mds[:, i] *= -1
if np.corrcoef(X_nmds[:, i], X_true[:, i])[0, 1] < 0:
X_nmds[:, i] *= -1
Finally, we plot the original data and both MDS reconstructions.
fig = plt.figure(1)
ax = plt.axes([0.0, 0.0, 1.0, 1.0])
s = 100
plt.scatter(X_true[:, 0], X_true[:, 1], color="navy", s=s, lw=0, label="True Position")
plt.scatter(X_mds[:, 0], X_mds[:, 1], color="turquoise", s=s, lw=0, label="MDS")
plt.scatter(X_nmds[:, 0], X_nmds[:, 1], color="darkorange", s=s, lw=0, label="NMDS")
plt.legend(scatterpoints=1, loc="best", shadow=False)
# Plot the edges
start_idx, end_idx = X_mds.nonzero()
# a sequence of (*line0*, *line1*, *line2*), where::
# linen = (x0, y0), (x1, y1), ... (xm, ym)
segments = [
[X_true[i, :], X_true[j, :]] for i in range(len(X_true)) for j in range(len(X_true))
]
edges = distances.max() / (distances + EPSILON) * 100
np.fill_diagonal(edges, 0)
edges = np.abs(edges)
lc = LineCollection(
segments, zorder=0, cmap=plt.cm.Blues, norm=plt.Normalize(0, edges.max())
)
lc.set_array(edges.flatten())
lc.set_linewidths(np.full(len(segments), 0.5))
ax.add_collection(lc)
plt.show()

Total running time of the script: (0 minutes 0.213 seconds)
Related examples
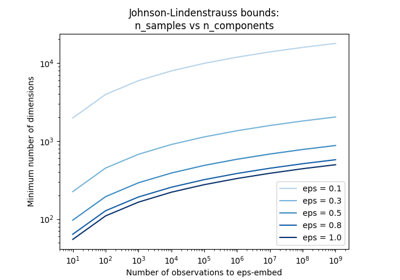
The Johnson-Lindenstrauss bound for embedding with random projections