Note
Go to the end to download the full example code. or to run this example in your browser via Binder
Lasso model selection via information criteria#
This example reproduces the example of Fig. 2 of [ZHT2007]. A
LassoLarsIC estimator is fit on a
diabetes dataset and the AIC and the BIC criteria are used to select
the best model.
Note
It is important to note that the optimization to find alpha with
LassoLarsIC relies on the AIC or BIC
criteria that are computed in-sample, thus on the training set directly.
This approach differs from the cross-validation procedure. For a comparison
of the two approaches, you can refer to the following example:
Lasso model selection: AIC-BIC / cross-validation.
References
# Authors: The scikit-learn developers
# SPDX-License-Identifier: BSD-3-Clause
We will use the diabetes dataset.
from sklearn.datasets import load_diabetes
X, y = load_diabetes(return_X_y=True, as_frame=True)
n_samples = X.shape[0]
X.head()
Scikit-learn provides an estimator called
LassoLarsIC that uses either Akaike’s
information criterion (AIC) or the Bayesian information criterion (BIC) to
select the best model. Before fitting
this model, we will scale the dataset.
In the following, we are going to fit two models to compare the values reported by AIC and BIC.
from sklearn.linear_model import LassoLarsIC
from sklearn.pipeline import make_pipeline
from sklearn.preprocessing import StandardScaler
lasso_lars_ic = make_pipeline(StandardScaler(), LassoLarsIC(criterion="aic")).fit(X, y)
To be in line with the definition in [ZHT2007], we need to rescale the AIC and the BIC. Indeed, Zou et al. are ignoring some constant terms compared to the original definition of AIC derived from the maximum log-likelihood of a linear model. You can refer to mathematical detail section for the User Guide.
import numpy as np
aic_criterion = zou_et_al_criterion_rescaling(
lasso_lars_ic[-1].criterion_,
n_samples,
lasso_lars_ic[-1].noise_variance_,
)
index_alpha_path_aic = np.flatnonzero(
lasso_lars_ic[-1].alphas_ == lasso_lars_ic[-1].alpha_
)[0]
lasso_lars_ic.set_params(lassolarsic__criterion="bic").fit(X, y)
bic_criterion = zou_et_al_criterion_rescaling(
lasso_lars_ic[-1].criterion_,
n_samples,
lasso_lars_ic[-1].noise_variance_,
)
index_alpha_path_bic = np.flatnonzero(
lasso_lars_ic[-1].alphas_ == lasso_lars_ic[-1].alpha_
)[0]
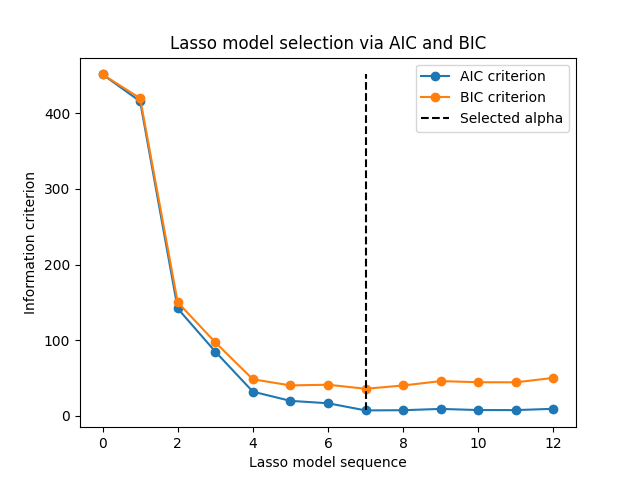
Now that we collected the AIC and BIC, we can as well check that the minima of both criteria happen at the same alpha. Then, we can simplify the following plot.
index_alpha_path_aic == index_alpha_path_bic
np.True_
Finally, we can plot the AIC and BIC criterion and the subsequent selected regularization parameter.
import matplotlib.pyplot as plt
plt.plot(aic_criterion, color="tab:blue", marker="o", label="AIC criterion")
plt.plot(bic_criterion, color="tab:orange", marker="o", label="BIC criterion")
plt.vlines(
index_alpha_path_bic,
aic_criterion.min(),
aic_criterion.max(),
color="black",
linestyle="--",
label="Selected alpha",
)
plt.legend()
plt.ylabel("Information criterion")
plt.xlabel("Lasso model sequence")
_ = plt.title("Lasso model selection via AIC and BIC")
Total running time of the script: (0 minutes 0.083 seconds)
Related examples