Vector Quantization Example

This example shows how one can use KBinsDiscretizer to perform vector quantization on a set of toy image, the raccoon face.

# Authors: The scikit-learn developers
# SPDX-License-Identifier: BSD-3-Clause

Original image

We start by loading the raccoon face image from SciPy. We will additionally check a couple of information regarding the image, such as the shape and data type used to store the image.

Note that depending of the SciPy version, we have to adapt the import since the function returning the image is not located in the same module. Also, SciPy >= 1.10 requires the package pooch to be installed.

try:  # Scipy >= 1.10
    from scipy.datasets import face
except ImportError:
    from scipy.misc import face

raccoon_face = face(gray=True)

print(f"The dimension of the image is {raccoon_face.shape}")
print(f"The data used to encode the image is of type {raccoon_face.dtype}")
print(f"The number of bytes taken in RAM is {raccoon_face.nbytes}")

The dimension of the image is (768, 1024)
The data used to encode the image is of type uint8
The number of bytes taken in RAM is 786432

Thus the image is a 2D array of 768 pixels in height and 1024 pixels in width. Each value is a 8-bit unsigned integer, which means that the image is encoded using 8 bits per pixel. The total memory usage of the image is 786 kilobytes (1 byte equals 8 bits).

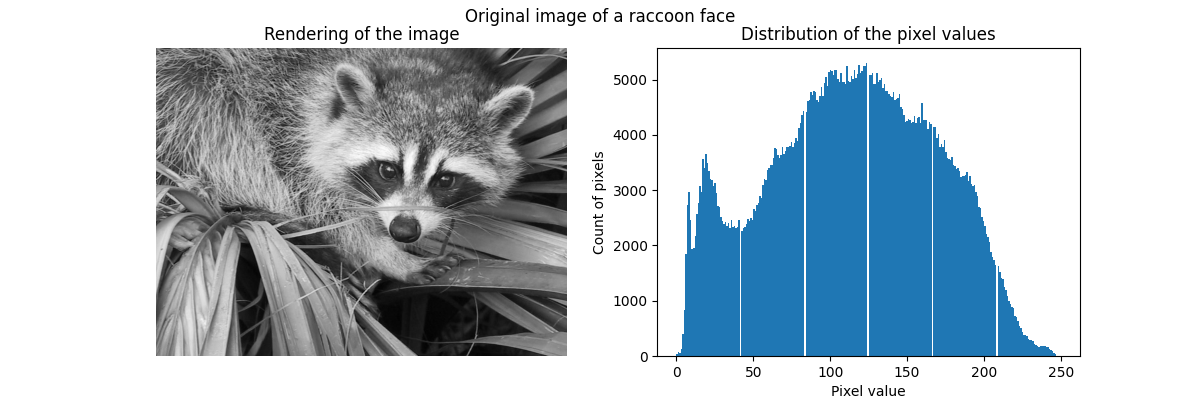
Using 8-bit unsigned integer means that the image is encoded using 256 different shades of gray, at most. We can check the distribution of these values.

import matplotlib.pyplot as plt

fig, ax = plt.subplots(ncols=2, figsize=(12, 4))

ax[0].imshow(raccoon_face, cmap=plt.cm.gray)
ax[0].axis("off")
ax[0].set_title("Rendering of the image")
ax[1].hist(raccoon_face.ravel(), bins=256)
ax[1].set_xlabel("Pixel value")
ax[1].set_ylabel("Count of pixels")
ax[1].set_title("Distribution of the pixel values")
_ = fig.suptitle("Original image of a raccoon face")

Compression via vector quantization

The idea behind compression via vector quantization is to reduce the number of gray levels to represent an image. For instance, we can use 8 values instead of 256 values. Therefore, it means that we could efficiently use 3 bits instead of 8 bits to encode a single pixel and therefore reduce the memory usage by a factor of approximately 2.5. We will later discuss about this memory usage.

Encoding strategy

The compression can be done using a KBinsDiscretizer. We need to choose a strategy to define the 8 gray values to sub-sample. The simplest strategy is to define them equally spaced, which correspond to setting strategy="uniform". From the previous histogram, we know that this strategy is certainly not optimal.

from sklearn.preprocessing import KBinsDiscretizer

n_bins = 8
encoder = KBinsDiscretizer(
    n_bins=n_bins,
    encode="ordinal",
    strategy="uniform",
    random_state=0,
)
compressed_raccoon_uniform = encoder.fit_transform(raccoon_face.reshape(-1, 1)).reshape(
    raccoon_face.shape
)

fig, ax = plt.subplots(ncols=2, figsize=(12, 4))
ax[0].imshow(compressed_raccoon_uniform, cmap=plt.cm.gray)
ax[0].axis("off")
ax[0].set_title("Rendering of the image")
ax[1].hist(compressed_raccoon_uniform.ravel(), bins=256)
ax[1].set_xlabel("Pixel value")
ax[1].set_ylabel("Count of pixels")
ax[1].set_title("Sub-sampled distribution of the pixel values")
_ = fig.suptitle("Raccoon face compressed using 3 bits and a uniform strategy")

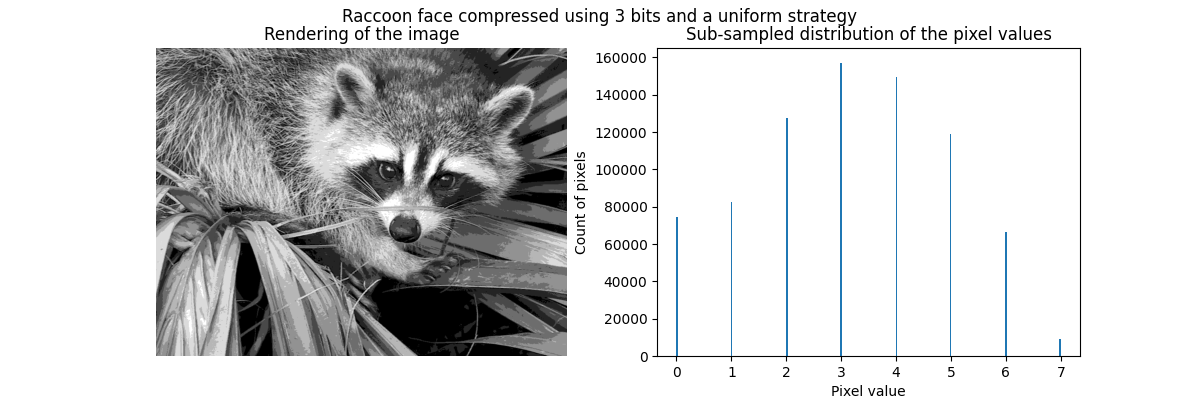
Qualitatively, we can spot some small regions where we see the effect of the compression (e.g. leaves on the bottom right corner). But after all, the resulting image is still looking good.

We observe that the distribution of pixels values have been mapped to 8 different values. We can check the correspondence between such values and the original pixel values.

bin_edges = encoder.bin_edges_[0]
bin_center = bin_edges[:-1] + (bin_edges[1:] - bin_edges[:-1]) / 2
bin_center

array([ 15.625,  46.875,  78.125, 109.375, 140.625, 171.875, 203.125,
       234.375])

_, ax = plt.subplots()
ax.hist(raccoon_face.ravel(), bins=256)
color = "tab:orange"
for center in bin_center:
    ax.axvline(center, color=color)
    ax.text(center - 10, ax.get_ybound()[1] + 100, f"{center:.1f}", color=color)

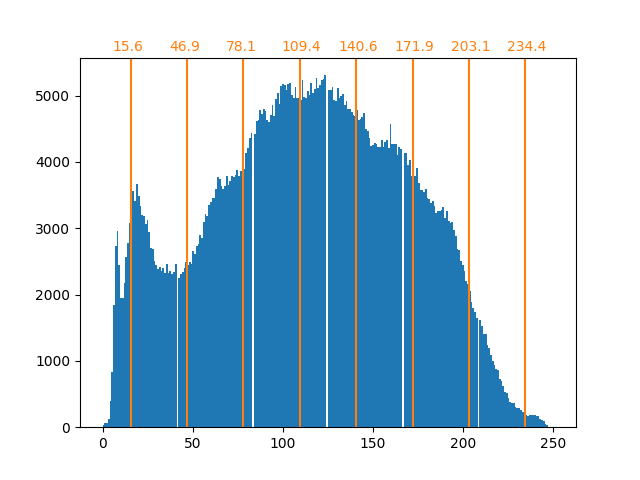
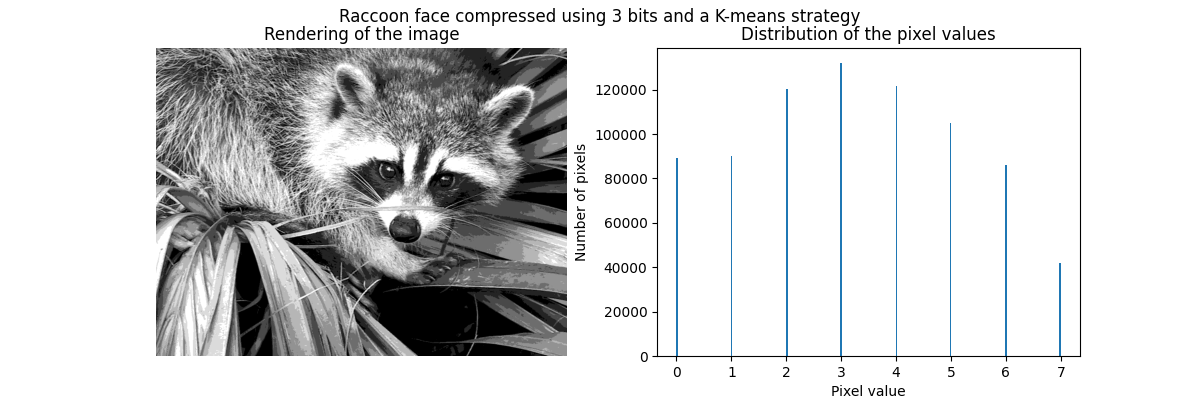
As previously stated, the uniform sampling strategy is not optimal. Notice for instance that the pixels mapped to the value 7 will encode a rather small amount of information, whereas the mapped value 3 will represent a large amount of counts. We can instead use a clustering strategy such as k-means to find a more optimal mapping.

encoder = KBinsDiscretizer(
    n_bins=n_bins,
    encode="ordinal",
    strategy="kmeans",
    random_state=0,
)
compressed_raccoon_kmeans = encoder.fit_transform(raccoon_face.reshape(-1, 1)).reshape(
    raccoon_face.shape
)

fig, ax = plt.subplots(ncols=2, figsize=(12, 4))
ax[0].imshow(compressed_raccoon_kmeans, cmap=plt.cm.gray)
ax[0].axis("off")
ax[0].set_title("Rendering of the image")
ax[1].hist(compressed_raccoon_kmeans.ravel(), bins=256)
ax[1].set_xlabel("Pixel value")
ax[1].set_ylabel("Number of pixels")
ax[1].set_title("Distribution of the pixel values")
_ = fig.suptitle("Raccoon face compressed using 3 bits and a K-means strategy")

bin_edges = encoder.bin_edges_[0]
bin_center = bin_edges[:-1] + (bin_edges[1:] - bin_edges[:-1]) / 2
bin_center

array([ 18.90885631,  53.34346583,  82.64447187, 109.28225276,
       134.70763101, 159.78681467, 185.17226834, 224.02069427])

_, ax = plt.subplots()
ax.hist(raccoon_face.ravel(), bins=256)
color = "tab:orange"
for center in bin_center:
    ax.axvline(center, color=color)
    ax.text(center - 10, ax.get_ybound()[1] + 100, f"{center:.1f}", color=color)

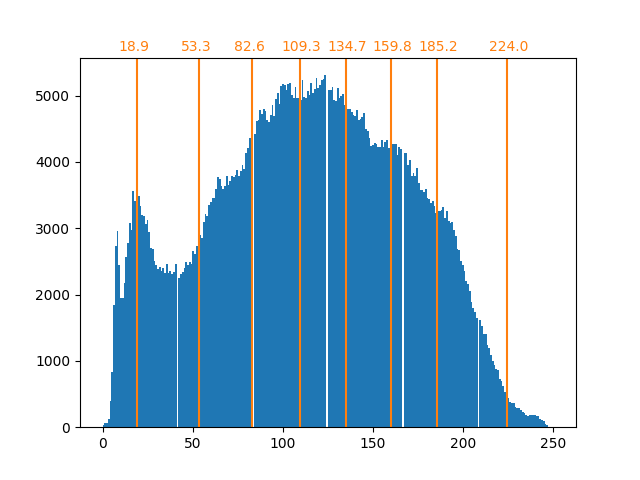
The counts in the bins are now more balanced and their centers are no longer equally spaced. Note that we could enforce the same number of pixels per bin by using the strategy="quantile" instead of strategy="kmeans".

Memory footprint

We previously stated that we should save 8 times less memory. Let’s verify it.

print(f"The number of bytes taken in RAM is {compressed_raccoon_kmeans.nbytes}")
print(f"Compression ratio: {compressed_raccoon_kmeans.nbytes / raccoon_face.nbytes}")

The number of bytes taken in RAM is 6291456
Compression ratio: 8.0

It is quite surprising to see that our compressed image is taking x8 more memory than the original image. This is indeed the opposite of what we expected. The reason is mainly due to the type of data used to encode the image.

print(f"Type of the compressed image: {compressed_raccoon_kmeans.dtype}")

Type of the compressed image: float64

Indeed, the output of the KBinsDiscretizer is an array of 64-bit float. It means that it takes x8 more memory. However, we use this 64-bit float representation to encode 8 values. Indeed, we will save memory only if we cast the compressed image into an array of 3-bits integers. We could use the method numpy.ndarray.astype. However, a 3-bits integer representation does not exist and to encode the 8 values, we would need to use the 8-bit unsigned integer representation as well.

In practice, observing a memory gain would require the original image to be in a 64-bit float representation.

Related examples

Image denoising using dictionary learning

Image denoising using dictionary learning

Color Quantization using K-Means

Color Quantization using K-Means

Recognizing hand-written digits

Recognizing hand-written digits

A demo of structured Ward hierarchical clustering on an image of coins

A demo of structured Ward hierarchical clustering on an image of coins