Note
Go to the end to download the full example code. or to run this example in your browser via Binder
Illustration of prior and posterior Gaussian process for different kernels#
This example illustrates the prior and posterior of a
GaussianProcessRegressor with different
kernels. Mean, standard deviation, and 5 samples are shown for both prior
and posterior distributions.
Here, we only give some illustration. To know more about kernels’ formulation, refer to the User Guide.
# Authors: The scikit-learn developers
# SPDX-License-Identifier: BSD-3-Clause
Helper function#
Before presenting each individual kernel available for Gaussian processes, we will define an helper function allowing us plotting samples drawn from the Gaussian process.
This function will take a
GaussianProcessRegressor model and will
drawn sample from the Gaussian process. If the model was not fit, the samples
are drawn from the prior distribution while after model fitting, the samples are
drawn from the posterior distribution.
import matplotlib.pyplot as plt
import numpy as np
def plot_gpr_samples(gpr_model, n_samples, ax):
"""Plot samples drawn from the Gaussian process model.
If the Gaussian process model is not trained then the drawn samples are
drawn from the prior distribution. Otherwise, the samples are drawn from
the posterior distribution. Be aware that a sample here corresponds to a
function.
Parameters
----------
gpr_model : `GaussianProcessRegressor`
A :class:`~sklearn.gaussian_process.GaussianProcessRegressor` model.
n_samples : int
The number of samples to draw from the Gaussian process distribution.
ax : matplotlib axis
The matplotlib axis where to plot the samples.
"""
x = np.linspace(0, 5, 100)
X = x.reshape(-1, 1)
y_mean, y_std = gpr_model.predict(X, return_std=True)
y_samples = gpr_model.sample_y(X, n_samples)
for idx, single_prior in enumerate(y_samples.T):
ax.plot(
x,
single_prior,
linestyle="--",
alpha=0.7,
label=f"Sampled function #{idx + 1}",
)
ax.plot(x, y_mean, color="black", label="Mean")
ax.fill_between(
x,
y_mean - y_std,
y_mean + y_std,
alpha=0.1,
color="black",
label=r"$\pm$ 1 std. dev.",
)
ax.set_xlabel("x")
ax.set_ylabel("y")
ax.set_ylim([-3, 3])
Dataset and Gaussian process generation#
We will create a training dataset that we will use in the different sections.
rng = np.random.RandomState(4)
X_train = rng.uniform(0, 5, 10).reshape(-1, 1)
y_train = np.sin((X_train[:, 0] - 2.5) ** 2)
n_samples = 5
Kernel cookbook#
In this section, we illustrate some samples drawn from the prior and posterior distributions of the Gaussian process with different kernels.
Radial Basis Function kernel#
from sklearn.gaussian_process import GaussianProcessRegressor
from sklearn.gaussian_process.kernels import RBF
kernel = 1.0 * RBF(length_scale=1.0, length_scale_bounds=(1e-1, 10.0))
gpr = GaussianProcessRegressor(kernel=kernel, random_state=0)
fig, axs = plt.subplots(nrows=2, sharex=True, sharey=True, figsize=(10, 8))
# plot prior
plot_gpr_samples(gpr, n_samples=n_samples, ax=axs[0])
axs[0].set_title("Samples from prior distribution")
# plot posterior
gpr.fit(X_train, y_train)
plot_gpr_samples(gpr, n_samples=n_samples, ax=axs[1])
axs[1].scatter(X_train[:, 0], y_train, color="red", zorder=10, label="Observations")
axs[1].legend(bbox_to_anchor=(1.05, 1.5), loc="upper left")
axs[1].set_title("Samples from posterior distribution")
fig.suptitle("Radial Basis Function kernel", fontsize=18)
plt.tight_layout()
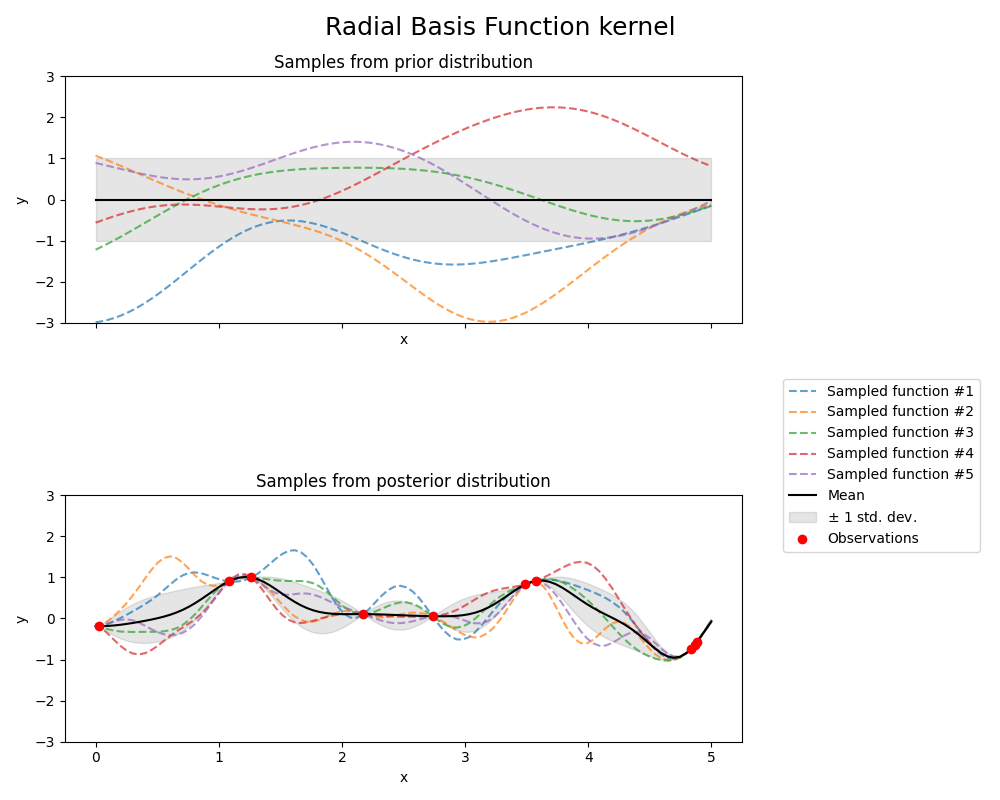
print(f"Kernel parameters before fit:\n{kernel})")
print(
f"Kernel parameters after fit: \n{gpr.kernel_} \n"
f"Log-likelihood: {gpr.log_marginal_likelihood(gpr.kernel_.theta):.3f}"
)
Kernel parameters before fit:
1**2 * RBF(length_scale=1))
Kernel parameters after fit:
0.594**2 * RBF(length_scale=0.279)
Log-likelihood: -0.067
Rational Quadratic kernel#
from sklearn.gaussian_process.kernels import RationalQuadratic
kernel = 1.0 * RationalQuadratic(length_scale=1.0, alpha=0.1, alpha_bounds=(1e-5, 1e15))
gpr = GaussianProcessRegressor(kernel=kernel, random_state=0)
fig, axs = plt.subplots(nrows=2, sharex=True, sharey=True, figsize=(10, 8))
# plot prior
plot_gpr_samples(gpr, n_samples=n_samples, ax=axs[0])
axs[0].set_title("Samples from prior distribution")
# plot posterior
gpr.fit(X_train, y_train)
plot_gpr_samples(gpr, n_samples=n_samples, ax=axs[1])
axs[1].scatter(X_train[:, 0], y_train, color="red", zorder=10, label="Observations")
axs[1].legend(bbox_to_anchor=(1.05, 1.5), loc="upper left")
axs[1].set_title("Samples from posterior distribution")
fig.suptitle("Rational Quadratic kernel", fontsize=18)
plt.tight_layout()
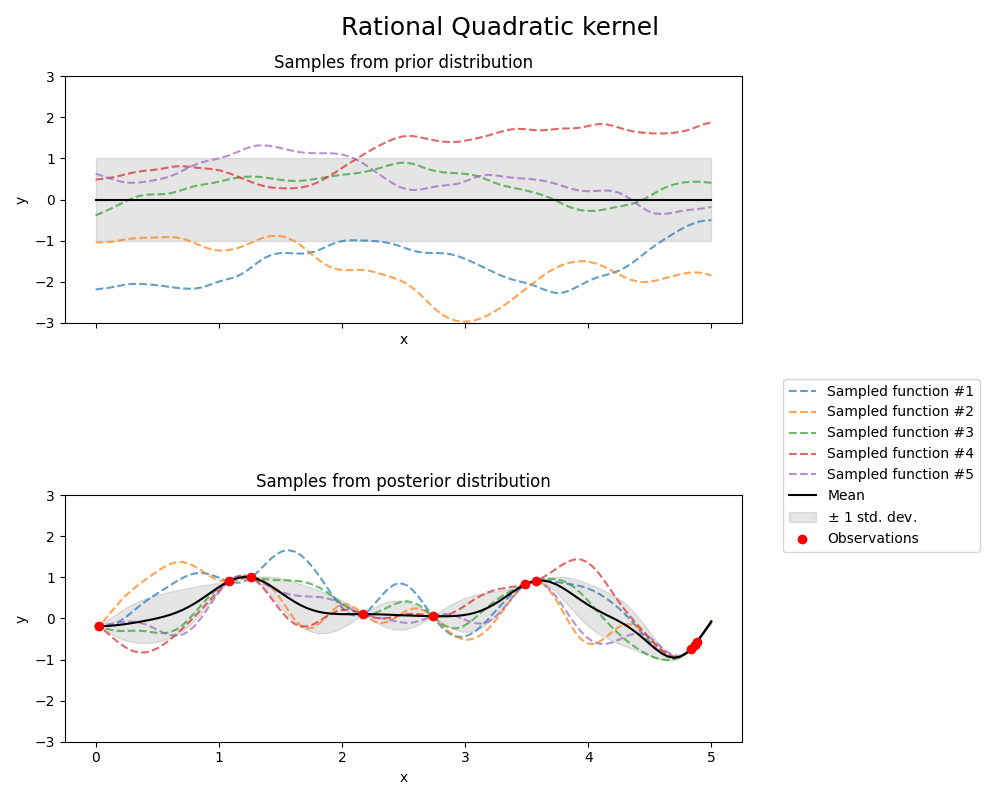
/opt/hostedtoolcache/Python/3.10.18/x64/lib/python3.10/site-packages/sklearn/gaussian_process/_gpr.py:533: RuntimeWarning:
covariance is not symmetric positive-semidefinite.
print(f"Kernel parameters before fit:\n{kernel})")
print(
f"Kernel parameters after fit: \n{gpr.kernel_} \n"
f"Log-likelihood: {gpr.log_marginal_likelihood(gpr.kernel_.theta):.3f}"
)
Kernel parameters before fit:
1**2 * RationalQuadratic(alpha=0.1, length_scale=1))
Kernel parameters after fit:
0.594**2 * RationalQuadratic(alpha=4.34e+08, length_scale=0.279)
Log-likelihood: -0.067
Exp-Sine-Squared kernel#
from sklearn.gaussian_process.kernels import ExpSineSquared
kernel = 1.0 * ExpSineSquared(
length_scale=1.0,
periodicity=3.0,
length_scale_bounds=(0.1, 10.0),
periodicity_bounds=(1.0, 10.0),
)
gpr = GaussianProcessRegressor(kernel=kernel, random_state=0)
fig, axs = plt.subplots(nrows=2, sharex=True, sharey=True, figsize=(10, 8))
# plot prior
plot_gpr_samples(gpr, n_samples=n_samples, ax=axs[0])
axs[0].set_title("Samples from prior distribution")
# plot posterior
gpr.fit(X_train, y_train)
plot_gpr_samples(gpr, n_samples=n_samples, ax=axs[1])
axs[1].scatter(X_train[:, 0], y_train, color="red", zorder=10, label="Observations")
axs[1].legend(bbox_to_anchor=(1.05, 1.5), loc="upper left")
axs[1].set_title("Samples from posterior distribution")
fig.suptitle("Exp-Sine-Squared kernel", fontsize=18)
plt.tight_layout()
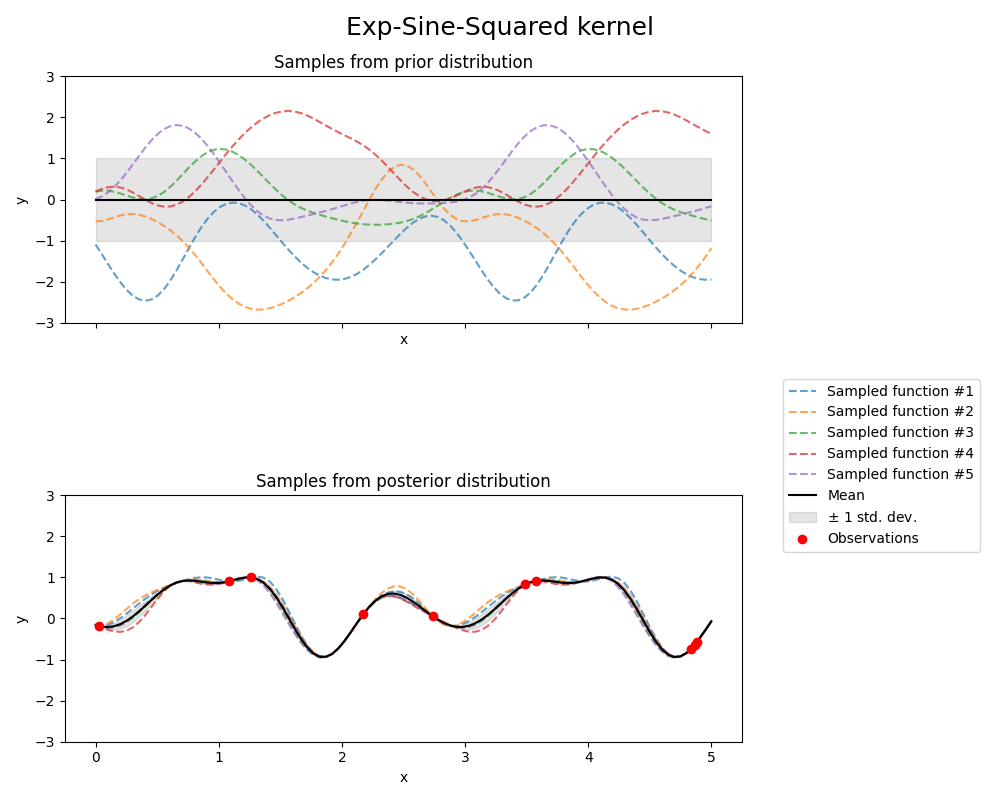
print(f"Kernel parameters before fit:\n{kernel})")
print(
f"Kernel parameters after fit: \n{gpr.kernel_} \n"
f"Log-likelihood: {gpr.log_marginal_likelihood(gpr.kernel_.theta):.3f}"
)
Kernel parameters before fit:
1**2 * ExpSineSquared(length_scale=1, periodicity=3))
Kernel parameters after fit:
0.799**2 * ExpSineSquared(length_scale=0.791, periodicity=2.87)
Log-likelihood: 3.394
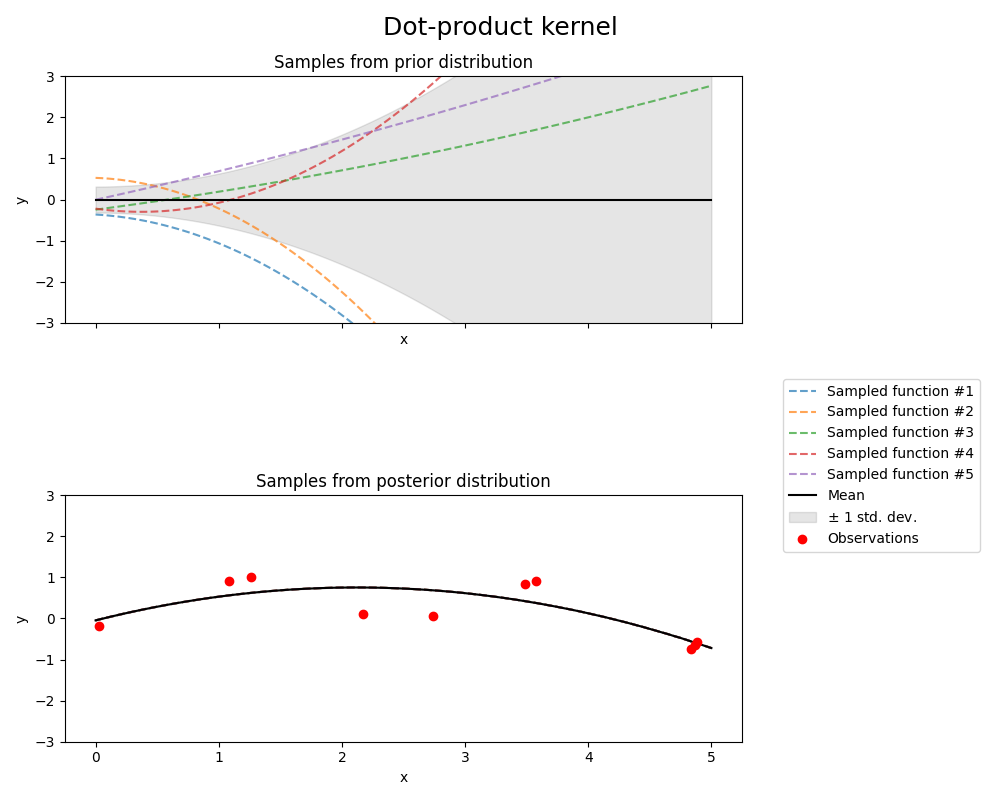
Dot-product kernel#
from sklearn.gaussian_process.kernels import ConstantKernel, DotProduct
kernel = ConstantKernel(0.1, (0.01, 10.0)) * (
DotProduct(sigma_0=1.0, sigma_0_bounds=(0.1, 10.0)) ** 2
)
gpr = GaussianProcessRegressor(kernel=kernel, random_state=0, normalize_y=True)
fig, axs = plt.subplots(nrows=2, sharex=True, sharey=True, figsize=(10, 8))
# plot prior
plot_gpr_samples(gpr, n_samples=n_samples, ax=axs[0])
axs[0].set_title("Samples from prior distribution")
# plot posterior
gpr.fit(X_train, y_train)
plot_gpr_samples(gpr, n_samples=n_samples, ax=axs[1])
axs[1].scatter(X_train[:, 0], y_train, color="red", zorder=10, label="Observations")
axs[1].legend(bbox_to_anchor=(1.05, 1.5), loc="upper left")
axs[1].set_title("Samples from posterior distribution")
fig.suptitle("Dot-product kernel", fontsize=18)
plt.tight_layout()
print(f"Kernel parameters before fit:\n{kernel})")
print(
f"Kernel parameters after fit: \n{gpr.kernel_} \n"
f"Log-likelihood: {gpr.log_marginal_likelihood(gpr.kernel_.theta):.3f}"
)
Kernel parameters before fit:
0.316**2 * DotProduct(sigma_0=1) ** 2)
Kernel parameters after fit:
1.83**2 * DotProduct(sigma_0=0.107) ** 2
Log-likelihood: -18098013535.226
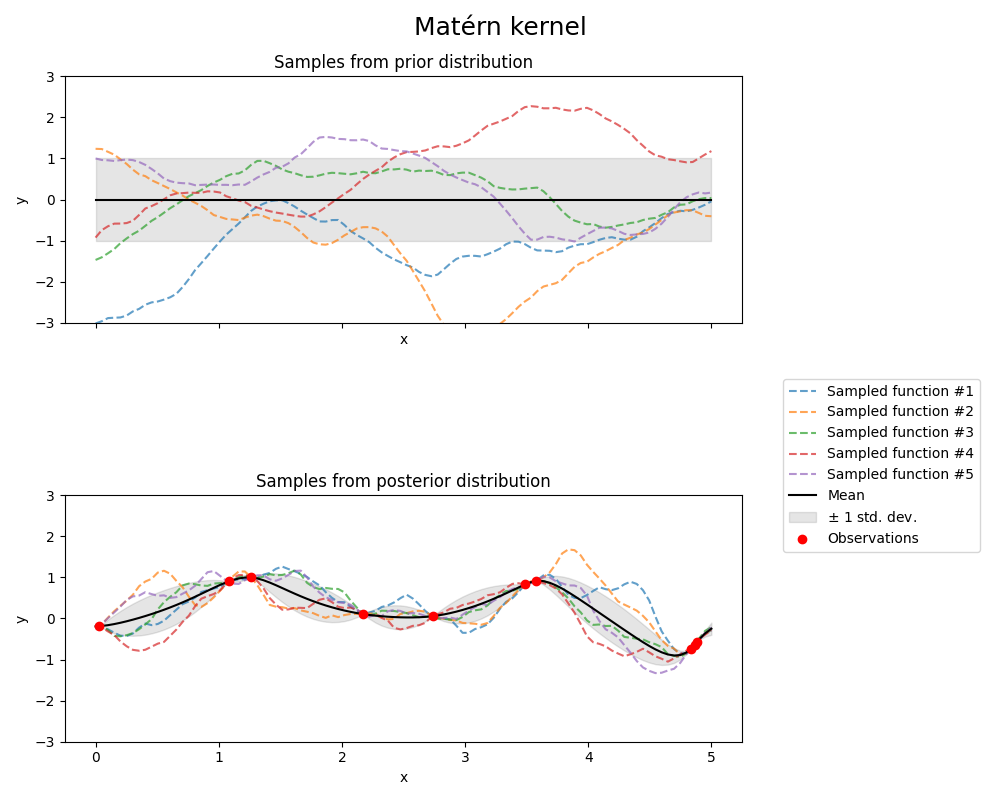
Matérn kernel#
from sklearn.gaussian_process.kernels import Matern
kernel = 1.0 * Matern(length_scale=1.0, length_scale_bounds=(1e-1, 10.0), nu=1.5)
gpr = GaussianProcessRegressor(kernel=kernel, random_state=0)
fig, axs = plt.subplots(nrows=2, sharex=True, sharey=True, figsize=(10, 8))
# plot prior
plot_gpr_samples(gpr, n_samples=n_samples, ax=axs[0])
axs[0].set_title("Samples from prior distribution")
# plot posterior
gpr.fit(X_train, y_train)
plot_gpr_samples(gpr, n_samples=n_samples, ax=axs[1])
axs[1].scatter(X_train[:, 0], y_train, color="red", zorder=10, label="Observations")
axs[1].legend(bbox_to_anchor=(1.05, 1.5), loc="upper left")
axs[1].set_title("Samples from posterior distribution")
fig.suptitle("Matérn kernel", fontsize=18)
plt.tight_layout()
print(f"Kernel parameters before fit:\n{kernel})")
print(
f"Kernel parameters after fit: \n{gpr.kernel_} \n"
f"Log-likelihood: {gpr.log_marginal_likelihood(gpr.kernel_.theta):.3f}"
)
Kernel parameters before fit:
1**2 * Matern(length_scale=1, nu=1.5))
Kernel parameters after fit:
0.609**2 * Matern(length_scale=0.484, nu=1.5)
Log-likelihood: -1.185
Total running time of the script: (0 minutes 1.835 seconds)
Related examples
Ability of Gaussian process regression (GPR) to estimate data noise-level
Bisecting K-Means and Regular K-Means Performance Comparison
Gaussian Processes regression: basic introductory example